Сколько возможно комбинаций в шахматах?

Вы когда-нибудь задумывались, сколько уникальных комбинаций можно расставить на шахматной доске?

Что ж, согласно основным источникам, существует популярный факт, что количество комбинаций в шахматах больше, чем количество атомов в наблюдаемой Вселенной. Это количество комбинаций называется числом Шеннона, и позже в этой статье вы увидите, как оно было разработано.

• Содержание
  • Сколько возможно шахматных комбинаций - объяснение числа Шеннона
  • Точное количество комбинаций развития игры за первые 5 ходов в шахматах
  • Может ли игра в шахматы продолжаться вечно?
  • Какая самая длинная шахматная партия?
  • Как английский математик Годфри Харди опровергает число Шеннона

Сколько возможно шахматных комбинаций - объяснение числа Шеннона

В 1950 году американский математик по имени Клод Шеннон опубликовал в журнале статью «Как запрограммировать компьютер для игры в шахматы». В этой статье он подсчитал, что количество комбинаций в шахматах будет равно 10¹²⁰. Это на самом деле превосходит количество атомов в известной Вселенной, которое оценивается от 10⁷⁸ до 10⁸² атомов. Это огромное число!

Но как мистер Клод придумал число 10¹²⁰? Ну, первое, что сделал Шеннон, это посмотрел несколько шахматных партий. После некоторого напряжённого размышления он заметил, что в среднем в любом положении находится около 30 легальных ходов, которые вы можете сделать. Возьмём для этого наглядный пример ниже:

У чёрных есть 37 вариантов ходов на выбор.

Вы можете попробовать сами посчитать. Возьмите любую случайную позицию из любой вашей шахматной партии и подсчитайте, сколько разрешённых ходов есть у каждой стороны. Должно быть около 30.

Теперь мы знаем, что в среднем каждая сторона может сделать 30 допустимых ходов. И если оба игрока сделают свой ход, у нас уже есть 30 × 30 = 900 возможных комбинаций. Впоследствии, если белые сделают ещё один ход, у нас будет 3 полных слоя, что даёт нам 30 × 30 × 30 = 27 000 шахматных комбинаций. {Примечание: другое название хода в шахматной терминологии — полуход}. Мы можем пойти ещё дальше к 4-му полуходу, который является второй парой ходов, и теперь у нас есть 30⁴ = 810 000 комбинаций. Надеюсь, вы уловили суть.

Теперь, средняя шахматная партия длится примерно 40 ходов, что и предложил Шеннон. Всего будет 80 полуходов для обоих игроков. А поскольку среднее количество возможных ходов, которые может сделать один человек, равно 30, следующее, что нужно было сделать Шеннону, — это просто представить сумму возможных комбинций в шахматах как 30⁸⁰≈ 10¹²⁰

Довольно просто, верно?

Конечно, это всего лишь оценка. Но вообще смысл есть.

На фото Клод Шеннон

Точное количество вариантов развития игры за первые 5 ходов в шахматах

Хотя Шеннон оценил количество шахматных комбинаций числом 10¹²⁰ но сегодня нет представления о точном количестве вариантов развития шахматной партии просто потому, что это число настолько огромно, что никто не будет прилагать усилий для подсчёта точного числа. Только Бог может сказать нам это. Тем не менее математики рассчитали первые 5 ходов (всего 10 полуходов). После того как каждый игрок передвинул фишку по 5 раз, можно было сыграть ровно 69 352 859 712 417 возможных партий.

Отработаем первую очередь ходов. На первом ходу у белых есть 20 возможных ходов на выбор.

Следующий ход за чёрными, у которых также есть 20 вариантов на выбор.

Следовательно, после того, как оба игрока сделают свой первый ход, существует 20 × 20 = 400 возможных расстановок доски уже после первого раунда ходов. После второй пары ходов (4 полухода) возможно 197 742 игры, а после третьей пары ходов — 121 миллион.

Таблица, показывающая количество возможных комбинаций для первых 5 ходов (10 полуходов)

Если вы посмотрите, как быстро росла последовательность только за первые 5 ходов, можете ли вы представить себе, сколько всего комбинаций в шахматах!

Может ли игра в шахматы продолжаться вечно?

Теоретически шахматная партия не может продолжаться вечно, так как правило пятидесяти ходов и трёхходовое повторение запрещают это. Это означает, что после 50 ходов если не было взятия или хода пешками, то партия должна быть объявлена ничейной или когда одна и та же позиция появляется три раза после трёхходового повторения. Даже если вы сделаете всё возможное, чтобы игра продолжалась вечно, вы неизбежно столкнётесь с правилом пятидесяти ходов или столкнётесь с повторением.

Какая самая длинная шахматная партия?

Теоретически, по мнению нескольких математиков, самая длинная шахматная партия может составлять около 11 800 полуходов. Конечно, этот расчёт связан с правилом 50 ходов и 3-х ходовым повторением, поскольку игра просто будет продолжаться вечно. Хотя есть разногласия с этим числом, на самом деле оно невелико.

Тем не менее, самая длинная шахматная партия, которую мы знаем на бумаге, длилась 269 ходов, а на ничью ушло 20 часов 15 минут (Николич-Арсович, Белград, 1989). Однако, тогда не работало правило 50 ходов, и поэтому партия продолжалась дольше, чем следовало бы. На самом деле, в те времена можно было делать 100 ходов без взятия фигур или ходов пешки.

Как английский математик Годфри Харди опровергает число Шеннона

Помните, мы говорили, что среднее количество ходов в шахматной партии составляет 40 ходов, которые Шеннон использует для расчёта своей оценки? Хотя это может показаться практичным, на бумаге это не так. Английский математик по имени Годфри Гарольд Харди попытался оценить количество возможных комбинации в шахматы, и его число было 10^^{10^50}

Оно читается как 10 в степени 10 в степени 50. Оценка Шеннона была бы абсолютно ничтожной по сравнению с этой цифрой.

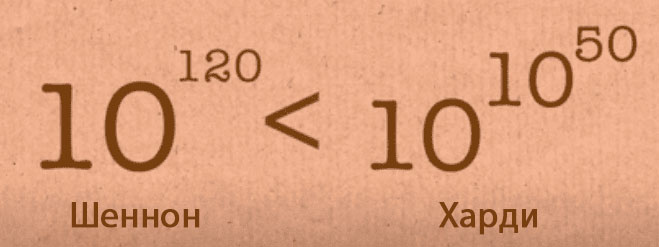
Но почему число Годфри больше, чем число Шеннона? Что ж, Шеннон говорил: «Это партии из 40 ходов», но хотя это может быть правдой в отношении обычных шахматных партий, он должен был принять во внимание другие нереалистичные партии. Например, игрок может решить НЕ ставить мат, если он находится в одном шаге от этого, а просто продолжить игру дальше. Это создаёт совершенно новое дерево возможностей. С другой стороны, мы никогда не будем уверены, близка ли оценка Харди, поскольку он не дал никаких расчётов.